Eur. Phys. J. B 23, 365-372 (2001)
https://doi.org/10.1007/s100510170056

Eigenvalues and eigenfunctions of a clover plate

Department of Physics, Clark University, Worcester, MA 01610, USA

Corresponding author: ^a tneicu@clarku.edu

Received: 12 February 2001
Revised: 17 April 2001
Published online: 15 October 2001

Abstract

We report a numerical study of the flexural modes of a plate using semi-classical analysis developed in the context of quantum systems. We first introduce the Clover billiard as a paradigm for a system inside which rays exhibit stable and chaotic trajectories. The resulting phase space explored by the ray trajectories is illustrated using the Poincare surface of section, and shows that it has both integrable and chaotic regions. Examples of the stable and the unstable periodic orbits in the geometry are presented. We numerically solve the biharmonic equation for the flexural vibrations of the Clover shaped plate with clamped boundary conditions. The first few hundred eigenvalues and the eigenfunctions are obtained using a boundary elements method. The Fourier transform of the eigenvalues show strong peaks which correspond to ray periodic orbits. However, the peaks corresponding to the shortest stable periodic orbits are not stronger than the peaks associated with unstable periodic orbits. We also perform statistics on the obtained eigenvalues and the eigenfunctions. The eigenvalue spacing distribution P(s) shows a strong peak and therefore deviates from both the Poisson and the Wigner distribution of random matrix theory at small spacings because of the 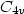symmetry of the Clover geometry. The density distribution of the eigenfunctions is observed to agree with the Porter-Thomas distribution of random matrix theory.